Morris Preorder Tree Traversal of a binary tree in C++

Post Views: 595

You are given a binary tree and you want to find the preorder traversal of the binary tree in C++.

There are several ways to do so. You can use recursion, stack. But if you want to perform preorder traversal without using recursion and stack, then you can go for Morris Preorder Traversal.

Algorithm:

Step 1: If the left child of the current node is null: then the print key of the current node and move to the right child of the current node.

Else: Find the preorder predecessor of the current and make its right child point to the current node. {

If the right child already points to the current node then make it null and set current=current->left.

Else If its right child is null: then set it to the current node and print the key of the current node and set current=current->left. }

Step 2: Repeat Step 1 until the current node is not null.

C++ Program to implement Morris Preorder Traversal

#include<bits/stdc++.h>
using namespace std;

struct node { 
  int key; 
  struct node *left,*right; 
  node(int x){
      key=x;
      left=right=NULL;
  }
}; 

// Morris Preorder Traversal Function 
void MorrisPreorderTraversal(struct node* root) 
{ 
  struct node *curr,*temp; 

  if (root == NULL) 
    return; 

  curr=root; 
  while (curr != NULL) { 

    if (curr->left == NULL)
    { 
      cout<<curr->key; 
      curr=curr->right; 
    } 
    else 
    { 
      temp = curr->left; 
      while (temp->right != curr && temp->right != NULL) 
        temp = temp->right; 
        
      if (temp->right == NULL)
      { 
          cout<<curr->key;
        temp->right = curr; 
        curr = curr->left; 
      } 

      else 
      { 
        temp->right = NULL; 
        curr=curr->right; 
      } 
    } 
  } 
} 

//main function 
int main() 
{ 

  struct node* root = new node(1); 
  root->left = new node(2); 
  root->right = new node(3); 
  root->left->left = new node(4); 
  root->left->right = new node(5); 
  root->left->right->right=new node(6);
  cout<<"Morris Preorder Traversal:"<<endl;
  MorrisPreorderTraversal(root); 

  return 0; 
}

Output:

Morris Preorder Traversal:
1 2 4 5 6 3

Time Complexity: O(n)

Also read: Morris Inorder Tree Traversal in C++

Full explanation with diagram:

Preorder Tree Traversal: It is a type of tree traversal in which first we visit Root then Left subtree and then Right Subtree of the graph.

Steps of Morris Preorder Tree Traversal algorithm:

Step 1:

If root->left==NULL {
print root->data
root=root->right
}
else{

Find preorder predecessor

Make preorder predecessor’s right child point to the curr node.

If the right child of the preorder predecessor is already pointing to the curr node{

Set the right child to NULL.

Move to the right child of the curr node.

}
else{

Set it to the curr node.

Print the data of curr node and move to the left child of the curr node.

}
}

Step 2:

Repeat step 1 until the root becomes NULL.

The flow of Morris Preorder Tree Traversal

Input tree:

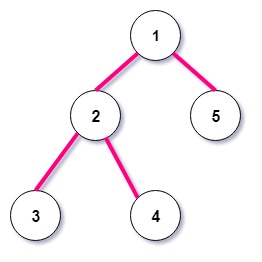
Iteration 1:

Iteration 2:

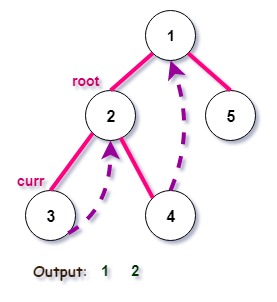
Iteration 3:

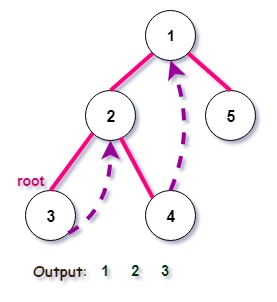
Iteration 4:

Iteration 5:

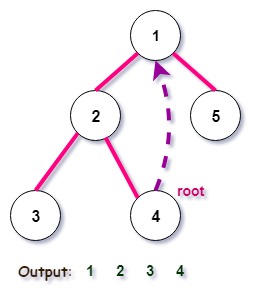
Iteration 6:

Iteration 7:

Program to implement Morris Preorder Tree Traversal in C++

#include<iostream> 
using namespace std;

/* Each node of a tree consists of a 1 data field and 2 links, 1 for left child and 1 for right child */
typedef struct Node
{ 
  int data; 
  Node* left; 
  Node* right; 
}Node; 

Node* new_node(int );
void morris_preorder_traversal(Node*);
Node* find_preorder_predecessor(Node*);

int main() 
{ 
  Node* root = new_node(1); 
  root->left = new_node(2); 
  root->right = new_node(5); 
  root->left->left = new_node(3); 
  root->left->right = new_node(4);
  /* this input tree is shown in above figure */ 

  cout<<"Morris Preorder Traversal of the graph: ";
  morris_preorder_traversal(root);
  
  return 0; 
} 

/* This function is used to create new node with the given data */
Node* new_node(int data) 
{ 
  Node* node = new Node; 
  node->data = data; 
  node->left = NULL; 
  node->right = NULL; 
  return node; 
}

Node* find_preorder_predecessor(Node* root)
{
  Node* curr=root->left; 
  while (curr->right && curr->right != root) 
    curr=curr->right; 
  
  return curr;
}

void morris_preorder_traversal(Node* root) 
{ 
  while (root) 
  { 
    if (root->left==NULL) 
    { 
      cout<<root->data<<" "; 
      root=root->right; 
    } 
    else
    { 
      /* Finding preorder predecessor */
      Node* curr=find_preorder_predecessor(root);

      /* If preorder predecessor's right child is already pointing to root */ 
      if (curr->right == root) 
      { 
        curr->right = NULL; 
        root=root->right; 
      } 
      else
      { 
        cout<<root->data<<" "; 
        curr->right = root; 
        root = root->left; 
      } 
    } 
  } 
}

Output:

Morris Preorder Traversal of the graph: 1 2 3 4 5

Time Complexity & Space Complexity

The Time Complexity and Space Complexity of the program is O(n) and O(1) respectively.

You may also read: