Morris Inorder Tree Traversal in C++

In this tutorial, we will learn Morris inorder tree traversal in C++. For learning morris inorder tree traversal first we should know about what is inorder tree traversal.

Inorder Tree Traversal:

It is a type of tree traversal in which first we visit Left subtree then Root and then Right Subtree of the graph.

Steps of Morris Inorder Tree Traversal algorithm:

1.  Initialize curr as root.

2. If curr->left == NULL {

print curr->data

curr = curr->right

}

else{

Find the inorder predecessor of curr

if predecessor->right==NULL {

predecessor->right=curr

curr=curr->left

}

else{

predecessor->right=NULL;

print curr->data

curr=curr->right

}

}

3. Repeat step 2 until the root becomes NULL.

Flow of Morris Inorder Tree Traversal

Input tree:

Iteration 1:

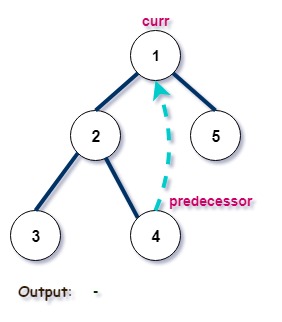
Iteration 2:

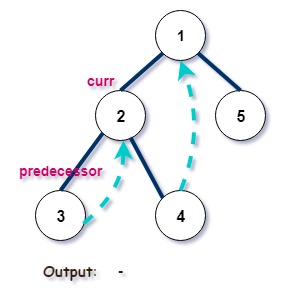
Iteration 3:

Iteration 4:

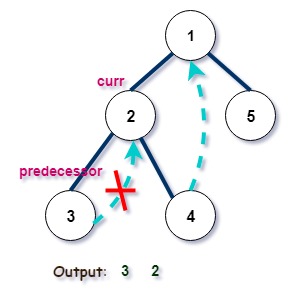
Iteration 5:

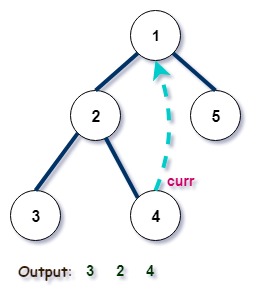
Iteration 6:

Iteration 7:

Program to implement Morris Inorder Tree Traversal in C++

#include<iostream> 
using namespace std;

/* Each node of a tree contains 1 data field and 2 links, 1 link to left child and 1 link to right child */
/* Typedef function is used to assign an alternative name to the existing datatype. Here, using typedef function we can write 'struct Node' as 'Node' */
typedef struct Node
{ 
  int data; 
  Node* left; 
  Node* right; 
}Node;
 
Node* new_node(int );
void morris_inorder_traversal(Node*);
Node* find_inorder_predecessor(Node*);

int main() 
{  
  Node* root = new_node(1); 
  root->left = new_node(2); 
  root->right = new_node(5); 
  root->left->left = new_node(3); 
  root->left->right = new_node(4);
 /* this input tree is shown in above figure */

  cout<<"\nMorris Inorder Traversal of the graph: ";
  morris_inorder_traversal(root);
  
  return 0; 
}
 
/* This function is used to create new node with the given data */
Node* new_node(int data) 
{ 
  Node* node = new Node; 
  node->data = data; 
  node->left = NULL; 
  node->right = NULL;
 
  return node; 
}

Node* find_inorder_predecessor(Node* curr)
{
	Node* predecessor=curr->left;
	while (predecessor->right != NULL && predecessor->right != curr) 
		predecessor=predecessor->right; 
		
		return predecessor;
}

void morris_inorder_traversal(Node* root) 
{ 
  Node *curr; 
  curr = root; 
  
  while (curr!=NULL) 
  { 
    /* if curr doesn't have left child */
    if (curr->left==NULL) 
    { 
      cout<<curr->data<<" "; 
      curr=curr->right; 
    } 
    else 
    { 
      	/* finding inorder predecessor */
		Node* predecessor=find_inorder_predecessor(curr);
			
      /* Make curr as the right child of its inorder predecessor */
      if(predecessor->right==NULL) 
      { 
        predecessor->right=curr; 
        curr=curr->left; 
      } 
      else 
      { 
        predecessor->right=NULL; 
        cout<<curr->data<<" "; 
        curr=curr->right; 
      }
    }
  }
} 

Output:

Morris Inorder Traversal of the graph: 3 2 4 1 5

Time Complexity & Space Complexity

The Time Complexity and Space Complexity of the program is O(n) and O(1) respectively.

 

You may also read:

1. Play Music in C++
2. Relative Sorting Algorithm and Implementation in C++