Matrix Inversion in C++
In this tutorial, we are going to learn about the matrix inversion.
Definition
Assuming that there is non-singular ( i.e. determinant(A) is not equal to zero) square matrix A, then an n × n matrix A-1 will exist, called the inverse of A such that:
AA-1 = A-1A = I, where I is the identity matrix.
Finding Matrix Inversion in C++
Firstly, we will see how to calculate the inversion of a matrix mathematically
The inverse can be obtained using the formula:
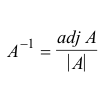
We will solve one example:

Now, let’s implement it on C++
#include<iostream>
using namespace std;
int main(){
int m[3][3]; //3x3 matrix
float d = 0;
cout<<"Enter elements of the matrix:\n";
for(int i = 0; i < 3; i++)
for(int j = 0; j < 3; j++)
std::cin>>m[i][j];
//finding determinant of the matrix
for(int i = 0; i < 3; i++)
d = d + (m[0][i] * (m[1][(i+1)%3] * m[2][(i+2)%3] - m[1][(i+2)%3] * m[2][(i+1)%3]));
if(d>0) //Condition to check if the derterminat is zero or not if zero than inverse dont exists
{
cout<<"\nInverse of the matrix is: \n";
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++)
std::cout<<((m[(j+1)%3][(i+1)%3] * m[(j+2)%3][(i+2)%3]) - (m[(j+1)%3][(i+2)%3] * m[(j+2)%3][(i+1)%3]))/ d<<"\t"; //finding adjoint and dividing it by determinant
std::cout<<"\n";
}
}
else std::cout<<"Inverse does'nt exist for this matrix";
return 0;
}
OUTPUT:
Enter elements of the matrix: 5 7 9 4 3 8 7 5 6 Inverse of the matrix is: -0.209524 0.0285714 0.27619 0.304762 -0.314286 -0.0380952 -0.00952381 0.228571 -0.12381
Also read,
Leave a Reply