Calculate Cosine Similarity in Python

Post Views: 808

In this tutorial, you will learn how to calculate Cosine similarity in Python

Introduction:

Here’s a short and straightforward example of how to calculate cosine similarity in Python. The following python code demonstrates how to calculate and find that out in Python. To understand this, firstly, we need to know what Cosine Similarity is:

Cosine Similarity is a measure that calculates the cosine of the angle between two non-zero vectors in an inner product space. In simpler words, it is a way to measure how similar two things are, based on their direction, not their size.

Formula:

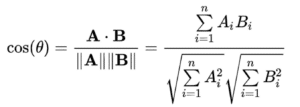
In the context of Python programming, it is often used to determine how similar two vectors are. It tells you how close these two lines are to each other.

To perform this follow this step-by-step procedure:

Import the NumPy library:

NumPy (Numerical Python) is an open-source Python library that is used for numerical and scientific computing. It helps in working with arrays. We have to use this library to perform further operations.

import numpy as np

This line imports the NumPy library. NumPy supports numerous mathematical functions, matrices, and arrays.

Define the ‘cosine_similarity’ Function:

def cosine_similarity(vector1, vector2):

This function takes two vectors (‘vector1’ and ‘vector2’) as input arguments.

Apply Dot Product to both the vectors:

dot_product = np.dot(vector1, vector2)

np.dot(vector1, vector2) calculates the dot product of the two vectors. np.dot(vector1, vector2)

The dot product is a way of multiplying two vectors to get a single number.
Imagine two lists of numbers (vectors) as having several items, like [1, 2, 3] and [4, 5, 6].
To get the dot product, we multiply the corresponding items. For example, 1 * 4 = 4, 2 * 5 = 10, 3 * 6 = 18
Now we add these results together 4 + 10 + 18 = 32. So, dot product is ’32’ in this case.

Calculate the Magnitude (Length) of Each Vector:

We calculate the magnitude of the vectors is calculated in this step

magnitude = np.linalg.norm(vector1) * np.linalg.norm(vector2)

This step calculates the product of the magnitudes (or lengths) of two vectors, ‘vector1’ and ‘vector2’

To get the magnitude:

For vector [1 , 2, 3]:
Square each item: 1^2 = 1, 2^2 = 4, 3^2 =9
Add these squares: 1 + 4 + 9 = 14
Take the square root of this sum: sqrt(14) ≈ 3.74

Do the same for vector [4, 5, 6]:
Squares: 4^2 = 14, 5^2 = 25, 6^2 = 3
Sum: 16 + 25 + 36 = 77
Square root: sqrt(77) ≈ 8.77

Multiply these magnitudes together: 3.74 * 8.77 ≈ 32.82. So, magnitude is 32.82 in this case.

Calculate the Cosine Similarity:

return dot_product / magnitude

Finally, we divide the dot product by the product of the magnitudes to get the cosine similarity.
Using our example values: 32 / 32.82 = 0.97
This value (0.97) tells us how similar the two vectors are. A value close to ‘1’ means they are very similar.

Creating Example Vectors:

vector1 and vector2 represent two example vectors as NumPy arrays. These arrays hold the coordinates of the vectors.

vector1 = np.array([1, 2, 3])
vector2 = np.array([4, 5, 6])

Calculating and Printing Cosine Similarity:

print(f"Cosine Similarity: {cosine_similarity(vector1, vector2)}")

The function ‘cosine_similarity’ calls with vector1 and vector2 as arguments.
The result, which is the cosine similarity between the two vectors, is then printed.

Complete Code:

import numpy as np

def cosine_similarity(vector1, vector2):
    dot_product = np.dot(vector1, vector2)
    magnitude = np.linalg.norm(vector1) * np.linalg.norm(vector2)
    return dot_product / magnitude

# Example vectors
vector1 = np.array([1, 2, 3]) 
vector2 = np.array([4, 5, 6])

# Calculate and print the cosine similarity
print(f"Cosine Similarity: {cosine_similarity(vector1, vector2)}")

Output:

Cosine Similarity: 0.9746318461970762

In Summary, this code calculated the cosine similarity in Python and returns it.

For a more in-depth explanation using additional functions and examples on calculating the cosine similarity in Python, you can refer to this:

How to calculate Cosine Similarity with sklearn Library

You may also refer to and learn: