Rabin Cryptosystem Implementation in C++

Rabin Cryptosystem is an asymmetric cryptography algorithm that is based on quadratic congruence. This cryptography technique involves a private key pair(p,q) and a public key n. This n is called ‘Blum Integer’ and the plain text x should always be:  1 < x < n. Its security like the RSA algorithm is determined by integer factorization (i.e. the decomposition of a composite integer into a product of smaller integers). The Rabin Cryptosystem has been mathematically proven to be computationally secure against a brute-force attack as long as the attacker is unable to get the correct factors.

Pre-requisites for implementing Rabin Cryptosystem in C++

In order to understand this cryptography technique one should know the following algorithms:

1. Extended Euclid Algorithm

2. Chinese Remainder Theorem

Basic knowledge of vectors/arrays is a must.

Key Generation in Rabin Cryptosystem:

Two prime numbers p and q form the private key pair, such that:

p≅3 (mod 4)

q≅3 (mod 4)

p ≠ q

n = p*q is the public key.

Encryption of the plain text :

The encrypter function takes two parameters, the plain text ‘m’ and the public key ‘n’.

It returns an integer value c, where c is the ciphertext.

The formula is c = (m²) mod n

int encrypter(int m, int n)
{
    int c = (m * m)%n;    // c = (m^2) mod n
    return c;
}

Utility functions used : Rabin Cryptosystem

int modulo (int a, int b)
{
    return a >= 0 ? a % b : ( b - abs ( a%b ) ) % b;
}

vector<int> Extended_Euclid(int a, int b)

{
    if (b>a) {
        int temp=a; a=b; b=temp;
    }
    int x=0;
    int y=1;
    int lastx=1;
    int lasty=0;
   
    while (b!=0) {
    
        int q= a/b;
        int temp1= a%b;
        a=b;
        b=temp1;
        int temp2 = x;
        x=lastx-q*x;
        lastx = temp2;
        int temp3 = y;
        y = lasty-q*y;
        lasty=temp3;
    
    }
    
    vector<int>arr(3);
    arr[0] = lastx;
    arr[1] = lasty;
    arr[2] = 1;
    return arr;
}

Decryption in the Rabin Cryptosystem in C++

Take the ciphertext c from the user and the private key pair (p,q).

Calculate mp and mq using the following formulae:

mp = C^{(p+1)/4 mod p}
mq = C^{(q+1)/4 mod q}

Find out a and b using the Extended Euclid Algorithm (a.p + b.q = 1)

Since the Rabin Cryptosystem is based on quadratic congruence there will be 4 possible roots after decryption.

r1,r2,r3,r4

Calculate root values rootp and rootq as follows:

int rootp = a*p*mq;
int rootq = b*q*mp;

calculate r = modulo((rootp+rootq), n);

calculate s = modulo((rootp-rootq),n);

Now, r1 = r

r2 = n – r

r3 = s

r4 = n-s

Convert the ascii value to text and Out of these 4 roots, one will be the plain text.

Below is the C++ implementation of the Rabin cryptosystem:

#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

int p = 151, q = 43; //private key pair(p,q) of the form 3 mod 4

int n = p * q;        //public key n

int encrypter(int m, int n)
{
    int c = (m * m)%n;    // c = (m^2) mod n
    return c;
}

int mod(int k, int b, int m) //chinese remainder theorem implementation
{
    int i=0;
    int a=1;
    vector<int> t;
    while(k>0){
        t.push_back(k%2);
        k=(k-t[i])/2;
        i++;
    }
    for(int j=0; j<i; j++){
        if(t[j]==1){
            a=(a*b)%m;
            b=(b*b)%m;
        } else{
            b=(b*b)%m;
        }
    }
    return a;
}

int modulo (int a, int b)
{
    return a >= 0 ? a % b : ( b - abs ( a%b ) ) % b;
}

vector<int> Extended_Euclid(int a, int b)
{
    if (b>a) {
        int temp=a; a=b; b=temp;
    }
    int x=0;
    int y=1;
    int lastx=1;
    int lasty=0;
    while (b!=0) {
        int q= a/b;
        int temp1= a%b;
        a=b;
        b=temp1;
        int temp2 = x;
        x=lastx-q*x;
        lastx = temp2;
        int temp3 = y;
        y = lasty-q*y;
        lasty=temp3;
    }
    vector<int>arr(3);
    arr[0] = lastx;
    arr[1] = lasty;
    arr[2] = 1;
    return arr;
}

int decrypter(int c, int p, int q)
{
    int mp = mod((p+1)/4, c, p);
    int mq = mod((q+1)/4, c, q);

    vector<int> arr = Extended_Euclid(p, q);
    int rootp = arr[0]*p*mq;
    int rootq = arr[1]*q*mp;
    double r = modulo((rootp+rootq), n);
    if( r < 128)
        return r;
    int negative_r = n - r;
    if (negative_r < 128)
        return negative_r;
    int s = modulo((rootp-rootq), n);
    if( s < 128)
        return s;
    int negative_s = n - s;
        return negative_s;

}

int main()
{
    vector<int>e; //vector to store the encrypted message
    vector<int>d; //vector to store the decrypted message
    string message ="CodeSpeedy is Cool!";
    cout << "Plain text: " << message << endl;
    int len = strlen(message.c_str());

    cout << "Encrypted text: ";
    for(int i = 0; i <= len; i++)
    {
        e.push_back(encrypter(message[i], n));
        cout << e[i];
    }

    cout << endl;

    for(int i = 0; i < len; i++)
    {
        d.push_back(decrypter(e[i], p, q));
    }
    cout << "Decrypted text: ";
    for(int i=0;i<d.size();i++)
      cout << char(d[i]);

    cout << endl;
    return 0;
}

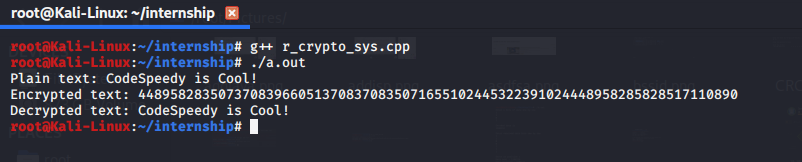
Output:

Also Read: Get all possible sublists of a list in Python